简单细分曲线

细分曲线

对于给定\(\mathbb{R}^2\)内一组有序点\(\{\mathbf{Q}_i\}_{i=0}^n\)，构成简单多边形，找到一条与之关联的光滑曲线。

Chaikin细分曲线（二次B-spline曲线细分）

拓扑规则：

• 点分裂成边（割角），老点被抛弃（逼近型）
• 新点老点重新编号

几何规则：

• \(\mathbf{Q}'_{2i}=\frac{1}{4}\mathbf{Q}_{i-1}+\frac{3}{4}\mathbf{Q}_i\)
• \(\mathbf{Q}'_{2i+1}=\frac{3}{4}\mathbf{Q}_i+\frac{1}{4}\mathbf{Q}_{i+1}\)

下图展示了经过5次Chaikin细分得到的细分曲线：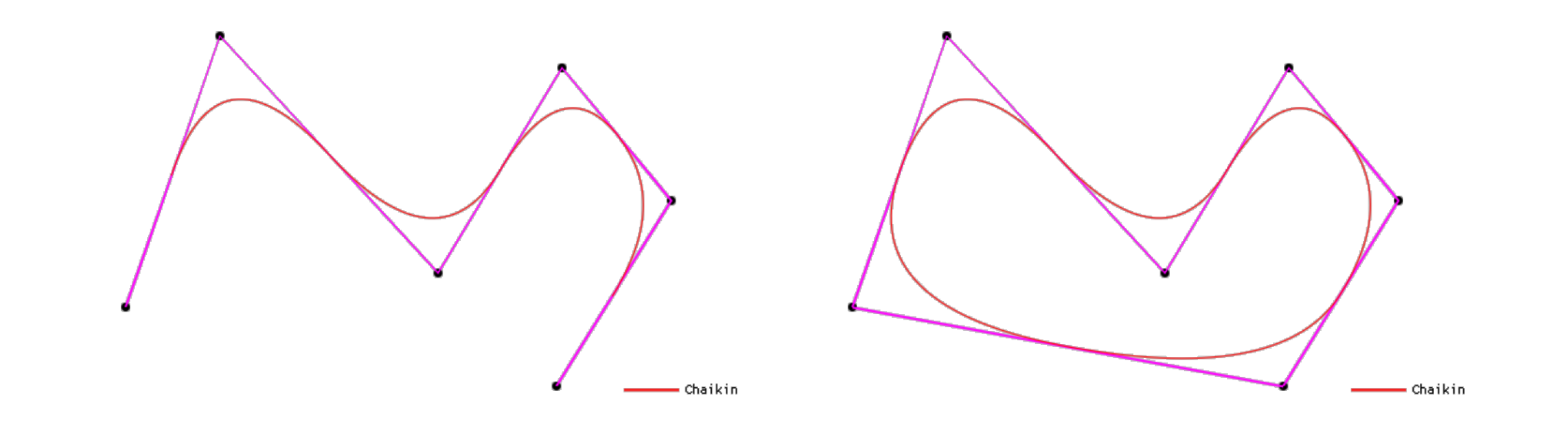

三次B-spline曲线细分

拓扑规则：

• 边分裂成两条新边

几何规则：

• \(\mathbf{Q}'_{2i}=\frac{1}{8}\mathbf{Q}_{i-1}+\frac{3}{4}\mathbf{Q}_i+\frac{1}{8}\mathbf{Q}_{i+1}\)
• \(\mathbf{Q}'_{2i+1}=\frac{1}{2}\mathbf{Q}_i+\frac{1}{2}\mathbf{Q}_{i+1}\)

下图展示了重复5次的“三次B样条”曲线细分得到的细分曲线：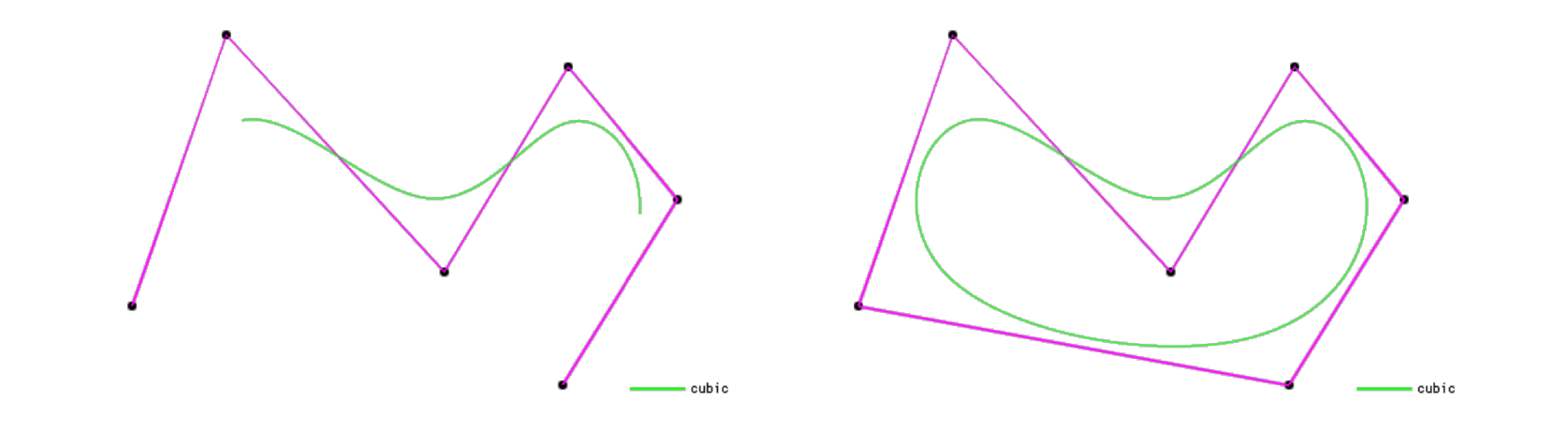

四点插值型细分（补角）

拓扑规则：

• 保留原有顶点
• 对每条边，增加一个新顶点

几何规则：

• \(\mathbf{Q}'_{2i+1}=\frac{\mathbf{Q}_i+\mathbf{Q}_{i+1}}{2}+\alpha\left(\frac{\mathbf{Q}_i+\mathbf{Q}_{i+1}}{2}-\frac{\mathbf{Q}_{i-1}+\mathbf{Q}_{i+2}}{2}\right)\)

下图展示了重复5次的四点插值细分得到的细分曲线：

主要代码

• Chaikin细分：

  std::vector<Ubpa::pointf2> Chaikin_subdivision(std::vector<Ubpa::pointf2 >* p, bool close) {
      std::vector<Ubpa::pointf2> newP;
      newP.clear();
      int n=p->size();
      if (close) {
          for (int i=0;i<p->size();++i) {
              newP.push_back(p->at((i-1+n)%n)*0.25f+p->at(i)*0.75f);
              newP.push_back(p->at(i)*0.75f+p->at((i+1)%n)*0.25f);
          }
      }
      if (!close) {
          newP.push_back(p->at(0)*0.75f+p->at(1)*0.25f);
          for (int i=1;i<p->size()-1;++i) {
              newP.push_back(p->at((i-1+n)%n)*0.25f+p->at(i)*0.75f);
              newP.push_back(p->at(i)*0.75f+p->at((i+1)%n)*0.25f);
          }
          newP.push_back(p->at((2*n-2)%n)*0.25f+p->at(n-1)*0.75f);
      }
      return newP;
  }

• 三次B样条细分曲线

  std::vector<Ubpa::pointf2> cubic_subdivision(std::vector <Ubpa::pointf2 >* p, bool close) {
      std::vector<Ubpa::pointf2> newP; newP.clear();
      int n=p->size();
      if (close) {
          for (int i=0;i<p->size();++i) { 
              newP.push_back(p->at((i-1+n)%n)*0.125f+p->at(i)*0.75f+p->at((i+1)%n)*0.125f); 
              newP.push_back(p->at(i)*0.5f+p->at((i+1)%n)*0.5f);
          }
      }
      if (!close) {
          newP.push_back(p->at(0)*0.5f+p->at(1)*0.5f); 
          for (int i=1;i<p->size()-1;++i) {
              newP.push_back(p->at((i-1+n)%n)*0.125f+p->at(i)*0.75f +p->at((i+1)%n)*0.125f);
              newP.push_back(p->at(i)*0.5f+p->at((i+1)%n)*0.5f); 
          }
      }
      return newP; 
  }

• 四点插值型细分曲线

  std::vector<Ubpa::pointf2> quad_subdivision(std::vector <Ubpa::pointf2>* p, bool close, float alpha=0.075) {
      std::vector<Ubpa::pointf2> newP; newP.clear();
      int n=p->size();
      if (close) {
          for (int i=0;i<p->size();++i) { 
              newP.push_back(p->at(i)); 
              newP.push_back((p->at(i)+p->at((i+1)%n))/2.0f+((p->at(i)+p->at((i+1)%n))/2.0f-(p->at((i-1+n)%n)+p->at((i+2)%n))/2.0f)*alpha);
          } 
      }
      if (!close) {
          for (int i=0;i<p->size()-1;++i) {
              newP.push_back(p->at(i)); 
              newP.push_back((p->at(i)+p->at((i+1)%n))/2.0f+((p->at(i)+p->at((i+1)%n))/2.0f-(p->at((i-1+n)%n)+p->at((i+2)%n))/2.0f)*alpha);
          } 
      }
      return newP; 
  }