三次样条函数
对于给定\(\mathbb{R}^2\)域内一组有序点\(\{\mathbf{Q}_i\}_{i=0}^n\),对应参数为\(\{t_i\}_{i=0}^n\),找到一组分段三次多项式函数插值每个数据点。
考虑插值点处\(C^2\)连续 (平滑顶点)
对于\(n+1\)个数据点,相邻两点之间用三次多项式表达,则有\(n\)段三次多项式,用待定系数的方式设第\(i(i=0,1,\dots,n)\)段向量型多项式函数为 \[\mathbf{P}_i(t)=a_{i,0}+a_{i,1}t+a_{i,2}t^2+a_{i,3}t^3\] 从上式可以看出总共\(4n\)个未知数,\(C^2\)连续需要满足约束条件:
每段多项式在端点处插值 \[\mathbf{P}_i(t_i)=\mathbf{Q}_i\qquad \mathbf{P}_i(t_{i+1})=\mathbf{Q}_{i+1}\qquad i = 0,1,\dots,n\]
中间点一阶导连续 \[\mathbf{P}'_{i-1}(t_i-0)=\mathbf{P}'_i(t_i+0)\qquad i=1,2,\dots,n-1\]
中间点二阶导连续 \[\mathbf{P}''_{i-1}(t_i-0)=\mathbf{P}''_i(t_i+0)\qquad i=1,2,\dots,n-1\]
这里总共\(4n-2\)个方程,还需要两个约束条件,这里我们选择首尾两点二阶导等于0,即自然边界条件:
\[\mathbf{P}''_0(t_0)=\mathbf{P}''_{n-1}(t_n)=0\qquad
i=1,2,\dots,n-1\] 这里我们引入中间变量弯矩,参考此文,可得每段多项式的表达式:
\[\mathbf{P}_i(t)=\frac{M_i}{6h_i}(t_{i+1}-t)^3+\frac{M_{i+1}}{6h_i}(t-t_i)^3+\left(\frac{Q_{i+1}}{h_i}-\frac{M_{i+1}h_i}{6}\right)(t-t_i)+\left(\frac{\mathbf{Q}_i}{h_i}-\frac{M_ih_i}{6}\right)(t_{i+1}-t)\]
其中\(h_i=t_{i+1}-t_i\),\(M\)是如下三对角线性系统的解,\(M_0=M_n=0\) \[\begin{equation}
\left(
\begin{array}{ccccc}
u_1 & h_1 & & &\\
h_1 & u_2 & h_2 & &\\
&\ddots&\ddots&\ddots&\\
&&h_{n-3}&u_{n-2}&h_{n-2}\\
&&&h_{n-2}&u_{n-1}
\end{array}
\right)\left(
\begin{array}{c}
M_1\\M_2\\\vdots\\M_{n-1}
\end{array}
\right)=\left(
\begin{array}{c}
v_1\\v_2\\\vdots\\v_{n-1}
\end{array}
\right)
\end{equation}\] 其中\(u_i=2(h_i+h_{i-1})\),\(v_i=\frac{6}{h_i}(\mathbf{Q}_{i+1}-\mathbf{Q}_i)-\frac{6}{h_{i-1}}(\mathbf{Q}_i-\mathbf{Q}_{i-1})\)
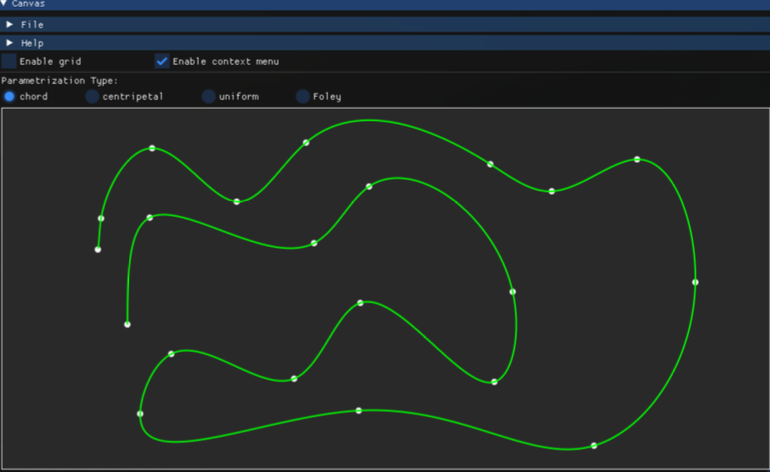
考虑插值点处\(C^0\)连续(角部顶点)
对于每一段给定插值点处的左导数\(f'_-\)和右导数\(f'_+\),加上插值该段的两点,4个未知数4个方程可以求解出该段的三次多项式函数:
例如在\([t_i,t_{i+1}]\)区间: \[\begin{equation}
\left\{
\begin{array}{ccccccccc}
a_{i,0} & + & a_{i,1}t_i & + & a_{i,2}t_i^2 & +
& a_{i,2}t_i^3 & = & \mathbf{Q}_i\\
a_{i,0} & + & a_{i,1}t_{i+1} & + & a_{i,2}t_{i+1}^2
& + & a_{i,2}t_{i+1}^3 & = & \mathbf{Q}_{i+1}\\
&&a_{i,1}&+&2a_{i,2}t_i&+&3a_{i,3}t_i^2&=&\mathbf{P}'_i(t_i+0)\\
&&a_{i,1}&+&2a_{i,2}t_{i+1}&+&3a_{i,3}t_{i+1}^2&=&\mathbf{P}'_{i+1}(t_i-0)
\end{array}
\right.
\end{equation}\] 求解该式可得到每段的三次多项式。 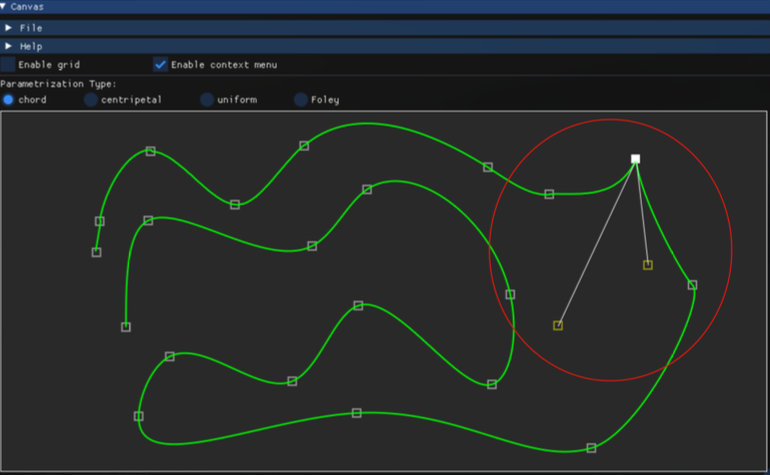
考虑插值点处\(G^1\)连续(直线点)
在角部顶点基础上保证一点的左导数与右导数方向在同一直线即可。即上面方程中\(\mathbf{P}'_i(t_i+0)=\lambda\mathbf{P}'_{i+1}(t_i-0)\)
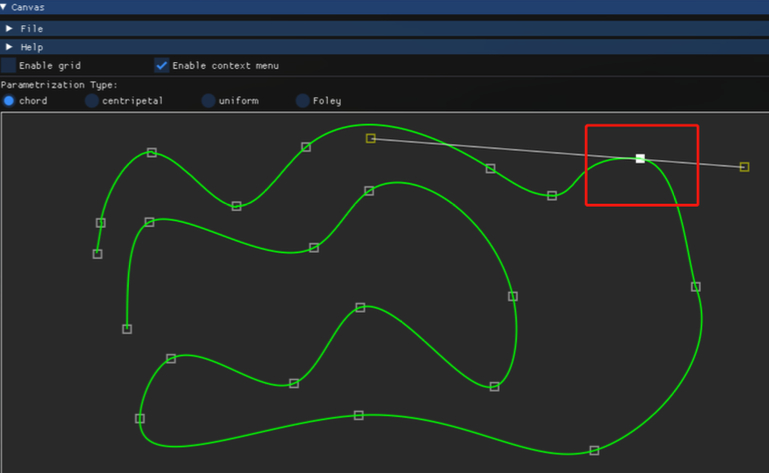
主要代码
高斯-塞德尔迭代求解三对角:
void GaussSeidel(std::vector<float> h, std::vector<float> u, std::vector<float> v, std::vector<float>* M) { std::vector<float> _M0 = *M; while (true) { for (int i=0; i<u.size(); ++i) { (*M)[i+1]=(v[i]-h[i]*(*M)[i]-h[i+1]*_M0[i+2])/u[i]; } // 迭代停止条件 if ((Eigen::VectorXf::Map((*M).data(),(*M).size())-Eigen::VectorXf::Map(_M0.data(),_M0.size())).norm()<EPSILON) { break; } _M0 = *M; } }求解给定导数后的分段样条:
if (validDerivative) { float x, y; auto A = [=](int i) -> Eigen::Matrix4f { Eigen::Matrix4f a; a << 1, t[i], t[i] * t[i], t[i] * t[i] * t[i], 1, t[i+1], t[i+1]*t[i+1], t[i+1]*t[i+1]*t[i+1], 0, 1, 2 * t[i], 3 * t[i] * t[i], 0, 1, 2 * t[i+1], 3*t[i+1]*t[i+1]; return a; }; auto B = [=](int i, int xy) -> Eigen::Vector4f { Eigen::Vector4f b; b << points[i][xy], points[i + 1][xy], (*derivative)[i].second[xy], (*derivative)[i + 1].first[xy]; return b; }; // 四维矩阵可用Eigen,不会影响交互延迟 Eigen::Vector4f ax = A(segment_index).colPivHouseholderQr().solve(B(segment_index, 0)); Eigen::Vector4f ay = A(segment_index).colPivHouseholderQr ().solve(B(segment_index, 1)); x = ax[0]+ax[1]*t0+ax[2]*t0*t0+ax[3]*t0*t0*t0; y = ay[0]+ay[1]*t0+ay[2]*t0*t0+ay[3]*t0*t0*t0; return Ubpa::pointf2(x, y);

