(增强篇) Bezier曲线拟合数据点的几何作图法

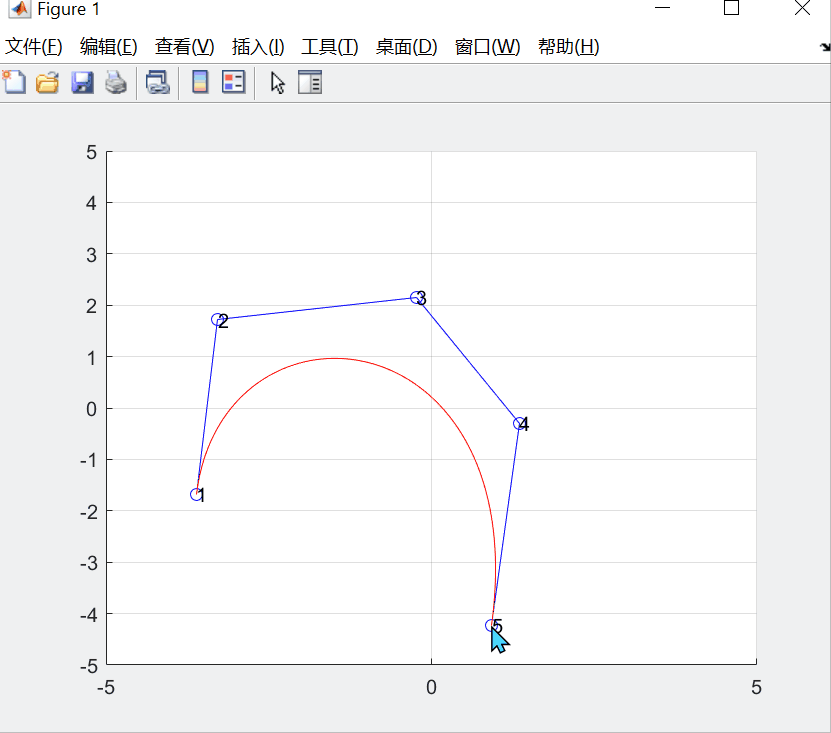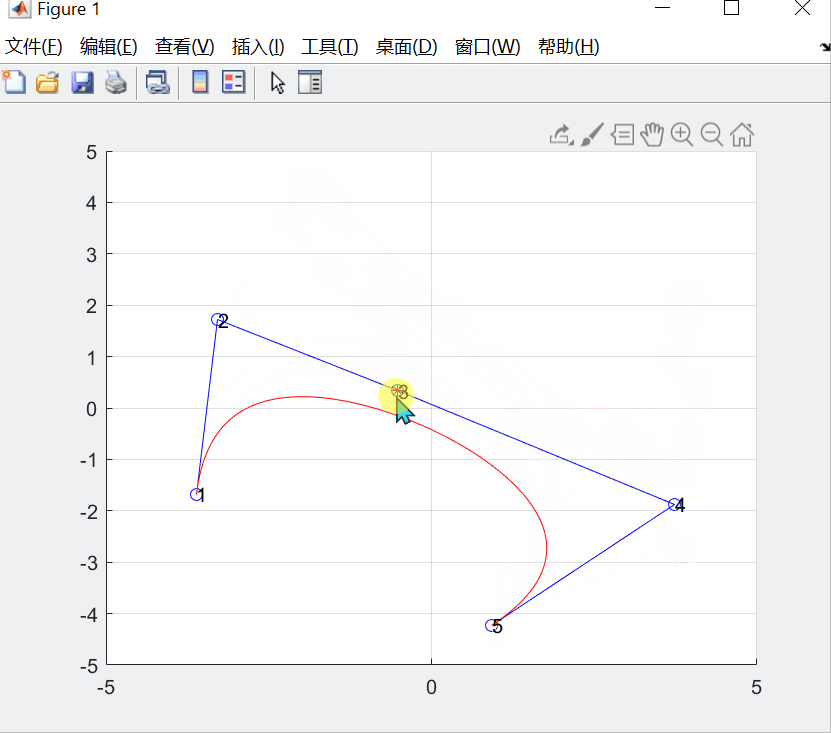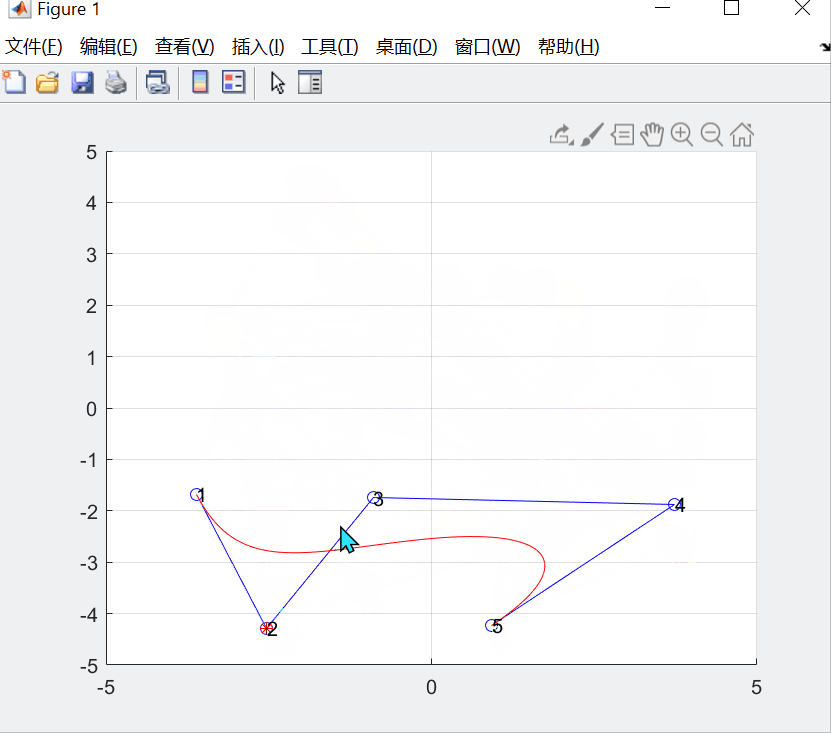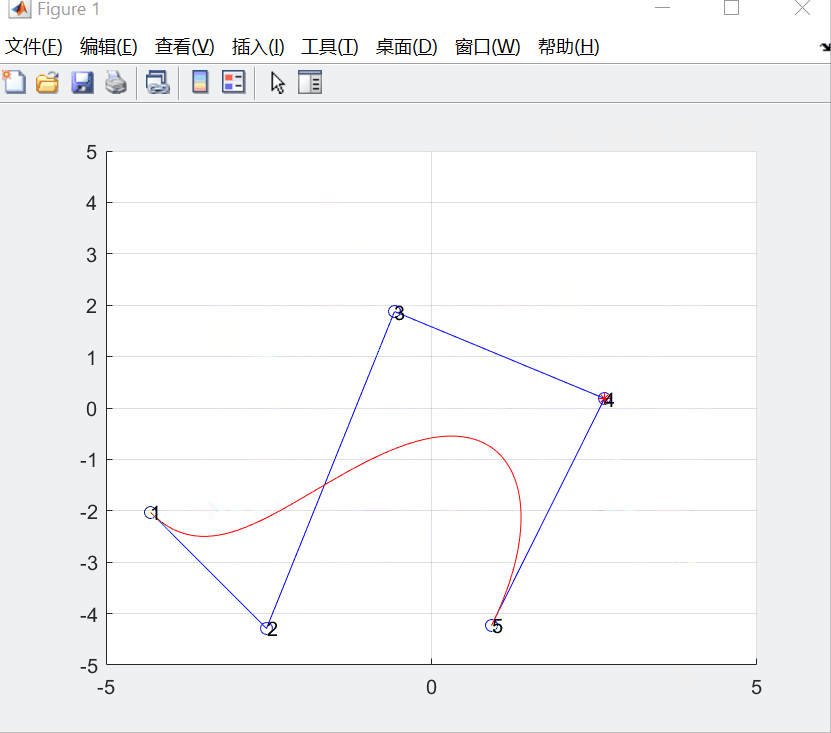
在之前的一篇 “Bezier曲线拟合数据点的几何作图法” 博客基础上添加鼠标移动控制顶点交互的功能。

交互选择控制顶点，并画出初始曲线

clear
close all
grid on,hold on
% axis equal
global ctrl_points h1 h_bezier;
[ctrl_points,h] = cqj_selectPoints(0);
for i = 0:0.01:1
    newData(:,int32(i*100)+1) = cqj_GetBezier3Point(ctrl_points,i);
end
h_bezier = plot(newData(1,:),newData(2,:),'-r');

h1 = plot(ctrl_points(1,1),ctrl_points(2,1),'r*');
set(h1,'visible','off');
text__ = cell(1,size(ctrl_points,2));
for i = 1:size(ctrl_points,2)
    text__{1,i} = num2str(i);
end

myText = text(ctrl_points(1,:),ctrl_points(2,:),text__);
set(gcf,'WindowButtonDownFcn',{@ButtonDownFcn,h,myText,h_bezier});
set(gcf,'WindowButtonUpFcn',@ButtonUpFcn);

Bezier曲线几何作图法

function [ data ] = cqj_GetBezier3Point(dataPoints,u)
% 得到曲线参数为u的数据点
% dataPoints：初始点 2xn
data = dataPoints;
while 1
    if size(data,2) == 1
        break;
    end
    temp = zeros(size(data,1),size(data,2)-1);
    for i = 1:size(data,2)-1
        temp(:,i) = (1-u)*data(:,i)+u*data(:,i+1);
    end
    data = temp;
end
end

处理鼠标响应事件

function ButtonUpFcn(~,~)
set(gcf, 'WindowButtonMotionFcn', '');    %取消鼠标移动响应
end

function ButtonMotionFcn(~,~,ind,h,myText,h_bezier)
global ctrl_points h1;
pt = get(gca,'CurrentPoint');    %获取当前点坐标
ctrl_points(:,ind) = [pt(1,1);pt(1,2)];

for i = 0:0.01:1
    newData(:,int32(i*100)+1) = cqj_GetBezier3Point(ctrl_points,i);
end
set(h_bezier,'XData',newData(1,:));
set(h_bezier,'YData',newData(2,:));
set(h,'xdata',ctrl_points(1,:));
set(h,'ydata',ctrl_points(2,:));
set(myText(ind),'position',[pt(1,1),pt(1,2),0]);
set(h1,'xdata',pt(1,1));
set(h1,'ydata',pt(1,2));
set(h1,'visible','on');
drawnow;
end

function ButtonDownFcn(~,~,h,myText,h_bezier)
global ctrl_points h1;
pt = get(gca,'CurrentPoint');    %获取当前点坐标
curpoint = [pt(1,1);pt(1,2)];  % 当前点坐标
curpoint_tr = curpoint*ones(1,size(ctrl_points,2)); %当前点坐标矩阵 每列一样
distance = vecnorm(curpoint_tr-ctrl_points);  %当前点坐标与每个控制点的距离构成的向量
if min(distance(:))<0.1  % 如果距离控制点比较近
    [~,ind] = find(distance==min(distance(:)));% 当前点最近的那个点
    set(h1,'xdata',ctrl_points(1,ind));
    set(h1,'ydata',ctrl_points(2,ind));
    set(h1,'visible','on');
    set(gcf,'WindowButtonMotionFcn',{@ButtonMotionFcn,ind,h,myText,h_bezier}); %设置鼠标移动响应
end
end

封装了一个选择点的方法

function [dataPoints,h] = cqj_selectPoints(isclose,x_axis,y_axis)

if ~exist('isclose','var')
    isclose = 1;
end

if ~exist('x_axis','var')
    x_axis = [-5,5];
end
if ~exist('y_axis','var')
    y_axis = [-5,5];
end
axis([x_axis,y_axis]);
grid on,hold on
questdlg('1.鼠标左键：选择新点   2.鼠标中键或右键：选择最后一个点','操作','ok','ok');
%% 从鼠标获取数据点
i = 0;
while 1
    i = i+1;
    tip = ['请选择第',num2str(i),'个数据点'];
    xlabel(tip);
    try
        [x,y,button] = ginput(1);
    catch
        return;
    end
    dataPoints(:,i) = [x;y];
    if i==1
        h = plot(dataPoints(1,:),dataPoints(2,:),'b-o');
    else
        set(h,'XData',dataPoints(1,:));
        set(h,'YData',dataPoints(2,:));
    end
    if button ~= 1
        xlabel('');
        break;
    end
end
if isclose
    set(h,'XData',[dataPoints(1,end) dataPoints(1,1)]);
    set(h,'YData',[dataPoints(2,end) dataPoints(2,1)]);
end
end

结果